Analysointivaiheessa aineistosta tuotetaan tietoa

Kun aineisto on kerätty, se tarkistetaan ja mahdollisesti täydennetään. Tarkistuksessa käydään vastaukset läpi ja tarvittaessa hylätään esimerkiksi puutteelliset vastaukset tai tulokset esimerkiksi silloin, jos esim. lomaketta ei ole täytetty huolellisesti. Joissakin tilanteissa aineistoa joudutaan täydentämään keräämällä sitä lisää.

Aineiston analysointi voi olla joko selittämiseen tai ymmärtämiseen pyrkivää (Hirsjärvi et al. 2013). Määrälliset tutkimukset pyrkivät yleensä selittämään ilmiöitä, ja niissä analysoidaan tuloksia usein tilastollisin menetelmin. Ymmärtämiseen pyrkivässä lähestymistavassa tavoitteena on tehdä päätelmiä. Aineiston analysoinnissa on menetelmästä huolimatta erittäin tärkeää kytkeä tulokset tutkielmassa käytettyyn teoriataustaan. Analysoituja tuloksia voi verrata teoriaan myös johtopäätöksissä.

Alla esitellään lyhyesti laadullisen aineiston analyysiä ja kattavammin määrällisen aineiston analyysiin soveltuvia tilastollisia menetelmiä.

Aineiston käsittelystä ja analysointiprosessin vaiheista voit lukea lisää Tiedelukutaidon perusteet -kurssin luvusta Tutkimusaineiston käsittely. Sieltä löydät myös lisää tietoa ja todelliseen tutkimukseen liittyvän esimerkin laadullisen aineiston analysoimisesta.

Laadulliset menetelmät

Laadullisissa menetelmissä aineistoon tutustutaan ensin perusteellisesti. Aineistosta poimitaan asioita, jotka toistuvat tai nousevat selkeästi esille. Usein havaintoja kootaan teemojen alle. Teemat voivat löytyä suoraan aineistosta tai ne voivat tulla tutkimuksen teoriasta. Ne ovat luokkia joihin havainnot voidaan jakaa. Havaintoyksikkö voi olla sana, lause tai ajatuskokonaisuus. Jos esimerkiksi tutkitaan luokan ilmapiiriä, niin havaintoyksikkö voisi olla sanat, joilla oppilaat kuvailevat ilmapiiriä. Tämän jälkeen sanat voitaisiin esimerkiksi jakaa positiivisiin, neutraaleihin ja negatiivisiin sanoihin ja jatkaa analyysia siitä pienempiin osiin. Jos teemat tai luokat tulevat suoraan teoriasta, havaintoyksiköt voi jakaa suoraan niihin.

Tutkimusraportissa kunkin teeman osalta tuodaan esille näytteitä aineistosta usein, jotta luotettavuus lisääntyy. Sitaattien käytössä tulee kuitenkin olla kriittinen ja pohtia jokaisen tarpeellisuutta. Laadullista analyysiä voi tukea kvantifioimalla aineistoa ja hyödyntämällä määrällisiä menetelmiä. Tällöin lasketaan esimerkiksi erilaisiin teemoihin kuuluvien havaintojen lukumäärä ja nostetaan esiin joitakin tunnuslukuja kuten frekvenssejä, joiden laskemisesta kerrotaan lisää seuraavaksi. Toisaalta on hyvä muistaa, että laadullisessa aineistossa yksittäiselläkin havaintoyksiköllä saattaa olla merkitystä, vaikkei se toistuisikaan aineistossa. (Saaranen-Kauppinen & Puusniekka 2006.)

Tilastolliset menetelmät

Tilastollisten menetelmien tarkoituksena on helpottaa määrällisessä tutkimuksessa kerätyn aineiston kuvailua, tulkitsemista ja arviointia. Usein tavoitteena on vertailla keskenään eri ryhmiä tai tutkia muuttujien välisiä riippuvuuksia. Tilastollisen menetelmän valintaan vaikuttavat mm. muuttujien mitta-asteikot, havaintojen määrä ja jakauma sekä tutkimuskysymys. Seuraavaksi esitellään tavallisimpia tilastollisia menetelmiä ja kerrotaan, millaisissa tapauksissa niitä kannattaa käyttää.

1. Ennen analysointia

Ennen varsinaisten analyysien aloittamista on hyvä käydä muuttujat läpi ja merkitä ylös, millä mitta-asteikolla kukin muuttuja on mitattu. Muuttujien mitta-asteikot on esitelty kokonaisuudessa Aineiston kerääminen ja tutkimusmenetelmät. Tässä yhteydessä kannattaa myös jo miettiä, mitä virhelähteitä tutkimuksessa voisi olla. Näin osaa tulkita ja tarvittaessa suhtautua varauksella tilastollisten menetelmien antamiin tuloksiin. Kokeellisessa tutkimuksessa voi pohtia, mitkä kaikki tekijät mahdollisesti vaikuttavat mittaustulosten luotettavuuteen, ja onko ei-tutkittavien muuttujien pitäminen samoina tutkimuksen aikana onnistunut. Otantatutkimuksissa taas tulee kiinnittää erityistä huomioita otoksen satunnaisuuteen. Jos esimerkiksi koulun ilmapiiriä koskevaan kyselyyn vastaavat ainoastaan tutkijan kaverit, saattavat tulokset olla erilaisia kuin silloin, jos vastaajat olisi arvottu koulun oppilasluettelosta.

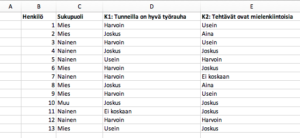
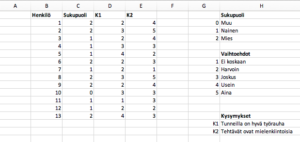
Tilastollisten menetelmien käyttämistä varten aineiston tulee yleensä olla taulukkomuodossa. Aineisto esitetään siten, että eri muuttujat ovat omina sarakkeinaan ja havainnot tulevat omille riveilleen (katso mallia alempana olevasta kuvasta). Joskus muuttujien sanalliset arvot kannattaa muuttaa numeerisiksi: esimerkiksi mielipideasteikon vastaukset ”täysin eri mieltä” – ”täysin samaa mieltä” voisi esittää numeroin 1 – 5. Tällöin on muistettava pitää kirjaa siitä, mikä numero vastaa mitäkin alkuperäistä vastausta. Tällainen numeerinen koodaus on tarpeen silloin, jos vastauksista halutaan laskea jotakin, esimerkiksi korrelaatiokertoimia tai keskiarvoja. Numeerinen koodaus voi olla järkevää myös silloin, kun aineistoa on paljon ja se on paperisilla lomakkeilla. Sanallisten vastausten esittäminen numeroina nimittäin nopeuttaa tietojen syöttämistä sähköiseen muotoon. Tutkimusaineisto alkuperäisessä muodossaan ja numeeriseksi koodattuna voisi näyttää esimerkiksi tältä:

 

 

 

Tässä materiaalissa annetaan ohjeita siihen, miten tilastollisia analyysejä voi toteuttaa Microsoft Excelillä. Monien tilastollisten testien tekeminen onnistuu kätevämmin varsinaisilla tilasto-ohjelmistoilla, joiden käyttäminen saattaa kuitenkin vaatia enemmän opettelua. Useat niistä ovat maksullisia (esim. SPSS), mutta netistä löytyy myös ilmaisia ohjelmistoja.

Excelin data-analyysissä käytettävä lisäosa ei yleensä ole automaattisesti näkyvissä, vaan se on ensin aktivoitava. Katso ohjeet aktivointiin (PDF).

2. Aineiston esittäminen ja kuvailu

Tutkimusaineistoa voidaan kuvata kuvioiden tai tilastollisten tunnuslukujen sekä niistä koottujen erilaisten taulukoiden avulla. Tilastolliset tunnusluvut antavat lukijalle tietoa aineistosta tiivistetyssä muodossa, kuvioiden avulla taas voidaan tarkastella havaintoarvojen vaihtelua eli jakaumaa kokonaisuudessaan. Aineiston raakadatan paikka ei ole varsinaisessa tekstissä, vaan sen voi halutessaan lisätä raportin liitteisiin. Katso lisäohjeita kuvioiden ja taulukoiden tekemiseen ja käyttämiseen kohdasta Tulosten visualisointi.

Jakaumat ja niiden esittäminen

Jakaumien esittämiseen liittyy käsite frekvenssi, joka kertoo, kuinka monta kertaa tietty arvo esiintyy havaintojen joukossa. Jos muuttuja on diskreetti eli epäjatkuva, sen jakaumaa voidaan kuvata laskemalla frekvenssit ja esittämällä ne pylväsdiagrammin muodossa. Excelissä tämä on helpointa tehdä luomalla pivot-taulukko, joka löytyy välilehdeltä Lisää (Insert). Pivot- taulukon kautta saa myös suoraan piirrettyä pylväsdiagrammin. Aiemmin esitellyn esimerkkidatan kysymyksen 1 vastausten frekvenssit sukupuolen mukaan jaoteltuna ja niistä muodostettu pylväsdiagrammi näyttävät pivot-taulukon avulla seuraavilta:

 

 

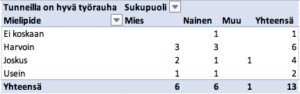
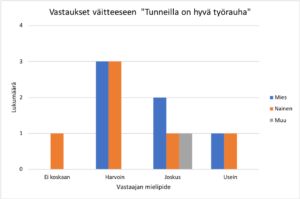
Tämä on itse asiassa esimerkki niin sanotusta ristiintaulukoinnista, jonka avulla tutkitaan muuttujien jakautumista ja niiden välisiä riippuvuuksia. Ristiintaulukoinnissa mittaustulokset tai esimerkiksi kyselyvastaukset esitetään taulukoituna eri ryhmien tai yleisemmin riippumattomien muuttujien mukaan. Edellisessä esimerkissä vastaukset taulukoitiin vastaajan sukupuolen mukaan, jolloin päästään vertaamaan eri sukupuolten edustajien vastausten jakautumista. Pivot-taulukkotoiminnolla olisi toki helposti voitu esittää myös vastausten jakauma kaikkien vastaajien osalta sukupuolesta riippumatta.

Jatkuvien muuttujien jakaumia kuvataan histogrammilla, joka muodostetaan luokittelemalla aineisto ja laskemalla luokitellut frekvenssit. Histogrammi eroaa pylväsdiagrammista siten, että pylvään korkeus kuvaa tietylle välille osuvien havaintojen määrää yksittäisen arvon esiintymismäärän sijaan. Histogrammissa pylväät ovat kiinni toisissaan muuttujan jatkuvuuden korostamiseksi. Excelissä on histogrammin tekemistä varten valmis funktio, joka löytyy valikosta Lisää (Insert) kuten muutkin kuvaajatyypit.

Tärkein jatkuva jakauma on normaalijakauma, jonka kuvaajaa kutsutaan myös Gaussin käyräksi. Siinä valtaosa arvoista keskittyy keskiarvon läheisyyteen. Monet ihmisen ominaisuuksiin liittyvät suureet, kuten pituus, paino ja reaktioajat, ovat luonnostaan normaalijakautuneita. Useissa tilastollisissa testeissä edellytetään, että tutkittava muuttuja on normaalijakautunut (tai ainakin likimain normaalijakautunut). Muuttujan normaalijakautuneisuutta voidaan arvioida piirtämällä histogrammi ja vertaamalla sen muotoa silmämääräisesti Gaussin käyrään. Alla olevassa kuvassa on histogrammi datasta, joka on muodostettu ottamalla 200 arvon satunnaisotos normaalijakaumasta, jonka keskiarvo on 100 ja keskihajonta 30 (keskiarvosta ja keskihajonnasta lisää seuraavaksi). Kuvassa nähdään normaalijakaumalle tyypillinen kellomainen muoto, ja lisäksi voidaan havaita, että valtaosa arvoista sijaitsee keskiarvon 100 lähettyvillä.

 

 

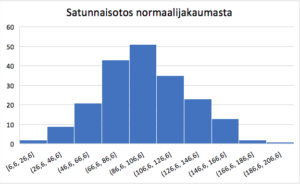
Vinojakauma tarkoittaa jakaumaa, jonka arvot ovat painottuneet jompaankumpaan päähän käytettävissä olevaa arvoasteikkoa. On myös olemassa kaksi- tai useampihuippuisia jakaumia. Usein tämä johtuu siitä, että tutkittavassa ilmiössä on kaksi tai useampi erilainen ryhmä yhdessä, jolloin näiden väliset erot selittävät jakauman painottumisen useampaan pisteeseen. Tämä on kuitenkin tutkijan tulkittava huolella ja etsittävä mahdolliset selittävät tekijät ilmiölle. (Salonen 2018.)

Tunnusluvut

Tilastollisia tunnuslukuja ovat esimerkiksi keskiluvut (keskiarvo, mediaani, moodi) ja hajontaluvut (varianssi, keskihajonta). Keskiluvut kuvaavat havaintoarvojen keskimääräistä sijaintia, ja hajontaluvut antavat kuvaa siitä, miten laajalle alueelle havainnot ovat levittäytyneet. Tunnusluvut kertovat havaintojen jakauman ominaisuuksista, ja monia niistä käytetään apuna tilastollisessa testaamisessa.

Keskiarvo kertoo jakauman keskikohdan, ja sen voi laskea välimatka- tai suhdeasteikolla mitatulle muuttujille. Mediaani on suuruusjärjestykseen järjestettyjen havaintojen keskimmäinen arvo, jota voi käyttää kuvaamaan aineistoa, kun muuttuja on vähintään järjestysasteikollinen. Moodi puolestaan kertoo havaintoaineistossa useimmin esiintyvän arvon, ja sen selvittäminen on mahdollista myös laatueroasteikollisille muuttujille. Riippuu aineiston rakenteesta, mikä keskiluku kuvaa sitä parhaiten. Esimerkiksi keskiarvo muuttuu helposti, jos aineistossa on jokin yksittäinen suuri tai pieni luku suhteessa muihin.

Tehtävä: Mikä keskiluku kuvaa mielestäsi parhaiten kuvitteellisen yrityksen Yritys X:n henkilöstön palkkoja (PDF) ja miksi? Katso sen jälkeen ratkaisuehdotus.

Varianssia ja keskihajontaa käytetään kuvaamaan havaintojen jakautumista keskiarvon ympäristöön. Suuri varianssi tarkoittaa, että havainnot ovat levittäytyneet laajalle alueelle, kun taas pieni varianssi kertoo, että havaintoarvot ovat keskimäärin melko samansuuruisia. Keskihajonta on varianssin neliöjuuri. Sen merkitys on käytännössä sama kuin varianssin, mutta keskihajonnan yksikkö on sama kuin alkuperäisen muuttujan, mikä on joskus kätevää.

Muuttujien normaalijakautuneisuutta voidaan tutkia histogrammin lisäksi tunnuslukujen huipukkuus ja vinous avulla. Täysin normaalijakautuneelle aineistolle kumpikin tunnusluku saa arvon 0. Positiiviset huipukkuuden arvot viittaavat normaalijakaumaa kapeampihuippuiseen jakaumaan ja negatiiviset taas normaalijakaumaa laakeampaan jakaumaan. Vinouden nollasta poikkeavat arvot tarkoittavat, että jakauma ei ole symmetrinen, vaan arvot ovat painottuneet kuvion jommallekummalle puolelle – negatiivisilla vinouden arvoilla havaintoja on normaalijakaumaan verrattuna enemmän kuvion oikealla puolella ja positiivisilla vastaavasti vasemmalla. Normaalijakautuneisuutta arvioitaessa kannattaa aina kuitenkin piirtää myös histogrammi.

Katso tunnuslukujen laskemiseen tarvittavat kaavat ja Excel-ohjeet (PDF).

3. Tilastolliset hypoteesit ja niiden testaaminen

Hypoteesien muodostaminen

Useat tilastolliset menetelmät perustuvat tilastollisten hypoteesien testaamiseen. Tilastollinen hypoteesi on tutkimuksen perusjoukkoa koskeva väite tai oletus, jonka paikkansapitävyyttä halutaan arvioida. Tilastollisen testaamisen tarkoituksena on etsiä vastauksia esimerkiksi seuraavanlaisiin kysymyksiin:

• Voidaanko otoksen perusteella tehdyt päätelmät yleistää koskemaan koko perusjoukkoa?
• Pätevätkö koejärjestelyssä esille tulleet ilmiöt laajemminkin kuin ainoastaan kokeessa mukana olleisiin yksilöihin?
• Onko todennäköistä, että tutkimuksessa havaitut vaikutukset johtuvat sattumasta? Onko esimerkiksi pituustutkimukseen valikoitunut sattumalta mukaan erityisen lyhyitä henkilöitä? Tai onko lannoitetutkimuksen eri koeasetelmissa ainoastaan sattumalta mukana eri nopeuksilla kasvavia kasviyksilöitä?

Jos tehty tutkimus on kokonaistutkimus, kaikki havaitut erot/vaikutukset ovat lähtökohtaisesti todellisia, mikäli mittarit ja mittausmenetelmä ovat luotettavia. Jos esimerkiksi tutkitaan, poikkeavatko tietyn ryhmän oikea- ja vasenkätisten opiskelijoiden kuvaamataidon arvosanat toisistaan ja aineistoon saadaan tiedot ryhmän jokaiselta opiskelijalta, ei tilastollista testausta tarvita. Jos sen sijaan halutaan tietää, poikkeavatko erikätisten opiskelijoiden kuvaamataidon arvosanat yleisesti toisistaan koko lukiossa tai esimerkiksi Rovaniemen kaikissa lukioissa, tulee käyttää tilastollista testaamista (sekä mahdollisimman sopivaa otantamenetelmää).

Tilastollisessa testaamisessa muodostetaan aluksi kaksi tilastollista hypoteesia: nollahypoteesi ja vastahypoteesi. Nollahypoteesi on yleensä muotoa ”ryhmien välillä ei ole eroa” tai ”käsittelyllä ei ollut vaikutusta”. Vastahypoteesi kuvaa nimensä mukaisesti vastakkaista väittämää, eli oletusta esimerkiksi ryhmien välisistä tai käsittelyn aiheuttamista eroista. Vastahypoteesit ja testaus voivat olla joko kaksisuuntaisia tai yksisuuntaisia. Kaksisuuntainen vastahypoteesi ei ota kantaa siihen, minkä suuntainen ryhmien välinen ero on. Aiemmin mainitussa esimerkissä kaksisuuntaisen vastahypoteesi voisi olla ”oikea- ja vasenkätisten arvosanat poikkeavat toisistaan”. Yksisuuntainen vastahypoteesi sen sijaan olettaa jotakin siitä, kumpaa ryhmää koskevat luvut ovat suurempia. Esimerkki tällaisesta vastahypoteeista on ”oikeakätisten arvosanat ovat korkeampia kuin vasenkätisten”. Kaksisuuntaista testiä käytetään, jos kumman tahansa ryhmän keskiarvo voi olla toista suurempi. Yksisuuntaista testiä käytetään, jos vain toisen ryhmän keskiarvo voi olla suurempi tai jos ollaan kiinnostuneita vain toisesta ryhmästä. Yksisuuntaisessa testissä pienemmät keskiarvoerot saavuttavat helpommin tilastollisesti merkitsevän tason. (Salonen 2018.)

On hyvä huomata, että tilastollinen hypoteesi on eri asia kuin kurssin alkupuolella mainittu (tutkimus)hypoteesi – usein nollahypoteesi saattaa olla nimenomaan tutkimushypoteesin vastakohta! Jos tutkimushypoteesina on esimerkiksi, että soittoharrastus parantaa koulumenestystä englannin kielen osalta, niin yksi tutkimusaineistoon liittyvä tilastollinen nollahypoteesi voisi olla, että soittoa harrastavien ja harrastamattomien englannin kielen arvosanoissa ei ole eroa. Yleensä hypoteesien testaamisessa toivotaankin, että nollahypoteesi saadaan kumottua. Tämä ei kuitenkaan tarkoita, etteikö nollahypoteesin jääminen voimaan eli ”ryhmien välillä ei ole eroa”-tulos voisi olla merkityksellinen (Salonen 2018).

Hypoteesien testaaminen

Tilastollinen testaaminen tapahtuu käytännössä laskemalla aineistosta testisuureita ja selvittämällä niiden perusteella, voidaanko nollahypoteesi hylätä. Testisuure mittaa sitä, miten hyvin tutkimuksessa saadut havainnot ja nollahypoteesi sopivat yhteen. Tilastollisessa testaamisessa selvitetään, kuinka todennäköistä on saada sellaisia testisuureen arvoja, kun on saatu, jos nollahypoteesi pitää paikkansa. Jos saadut arvot ovat riittävän epätodennäköisiä, tutkimusaineiston sanotaan sisältävän todisteita nollahypoteesia vastaan. (Mellin 2007.)

Mitä sitten tarkoittaa ”riittävän epätodennäköinen”, eli milloin nollahypoteesi voidaan hylätä? Tämä riippuu siitä, kuinka suuren erehtymisriskin tutkija on valmis ottamaan. Tilastollisten menetelmien avulla ei koskaan voida sanoa täysin varmasti, onko hypoteesi totta vai ei. Testauksessa voi käydä niin, että nollahypoteesi hylätään, vaikka se todellisuudessa pitääkin paikkansa. Tätä kutsutaan hylkäysvirheeksi tai tyypin I virheeksi. Hyväksymisvirhe eli tyypin II virhe puolestaan tarkoittaa, että nollahypoteesi hyväksytään silloin, kun se ei ole totta. Käytännössä hylkäysvirheen sattuessa ”löydetään” tutkimustulos, jota ei ole oikeasti olemassakaan. Hyväksymisvirhe sen sijaan johtaa tilanteeseen, jossa tutkimuksessa ”ei löydetty mitään”. Tätä pidetään yleensä vähemmän vaarallisena, sillä jos käsittelyn vaikutus tai ryhmien välinen ero todella on olemassa, sen uskotaan löytyvän myöhemmissä tutkimuksissa.

Tilastollisessa testaamisessa pyritään siis välttämään ensisijaisesti hylkäysvirheen tekemistä. Näin ollen tilastollinen päätöksenteko kytketään yleensä hylkäysvirheen todennäköisyyteen, jota kutsutaan testin merkitsevyystasoksi. Testin merkitsevyystaso kertoo siis riskin sille, että nollahypoteesi hylätään virheellisesti. Käytännössä testauksessa lasketaan yleensä niin sanottu p-arvo, joka kertoo pienimmän merkitsevyystason, jolla nollahypoteesin voi hylätä. Pienet p-arvot tarkoittavat, että havainnot eivät todennäköisesti johdu sattumasta. (Mellin 2007.)

Yleensä tilastotieteessä käytetään seuraavia merkitsevyystasoja ja niihin liittyviä tulkintoja:

• 5 % merkitsevyystaso: jos p-arvo < 0,05, niin tulos on tilastollisesti melkein (heikosti) merkitsevä
• 1 % merkitsevyystaso: jos p-arvo < 0,01, niin tulos on tilastollisesti merkitsevä
• 0,1 % merkitsevyystaso: jos p-arvo < 0,001, niin tulos on tilastollisesti erittäin merkitsevä. (Salonen 2018).

Tilastollisten testien tekeminen etenee seuraavasti:

• Määritellään nollahypoteesi ja vastahypoteesi.
• valitaan oikea tilastollinen testi. Tilastollisen testin valintaan annetaan ohjeita seuraavaksi.
• Valitaan merkitsevyystaso.
• Tehdään testi ja selvitetään p-arvo.
• Tulkitaan p-arvo. Jos p-arvo on pienempi kuin valittu merkitsevyystaso (yleensä < 0,05), hylätään nollahypoteesi ja vastahypoteesi astuu voimaan.
• Esitetään raportissa yhteenveto siitä, mitä tilastollisella testillä saadaan selville testisuureesta (esimerkkejä tilastollisten testien kohdalla). (Salonen 2018.)

P-arvoja tulkitessa kannattaa tiedostaa, että p-arvo ei kerro mitään eron tai vaikutuksen suuruudesta. Usein erotetaankin toisistaan tilastollinen merkitsevyys ja tieteellinen merkittävyys. Suurilla otoksilla voidaan saada hyvin pieniä p-arvoja silloinkin, kun ryhmien välinen ero on erittäin pieni. Tällöin tulos on kylläkin tilastollisesti merkitsevä, mutta ei käytännön kannalta merkittävä. Merkittävyyden arvioinnissa voidaan käyttää apuna efektikokoa, jolla mitataan itse ilmiön voimakkuutta. Efektikoon laskemiseen on useita tapoja, joista tässä esitellään Cohenin d- mittari. Se perustuu ryhmien keskiarvoihin ja keskihajontojen keskiarvoihin, ja sitä voi käyttää verrattaessa kahta ryhmää keskenään. Efektikoolle voidaan määrittää seuraavat raja- arvot:

• ≥ 0,2 on tilastollisesti heikosti merkittävä
• ≥ 0,50 on tilastollisesti merkittävä
• ≥ 0,80 on tilastollisesti erittäin merkittävä.

Efektikokoa raportoidessa kerrotaan efektikokona luvun itseisarvo; merkkiä käytetään kertomaan kumpaan suuntaan ilmiö vaikuttaa. Negatiivinen efektikoko tarkoittaa tutkitun asian negatiivista vaikutusta. Katso tarvittavat kaavat ja Excel-esimerkki efektikoon laskemisesta ja tulkitsemisesta. (Salonen 2018).

Tilastollisia testejä

a) Kahden riippumattoman otoksen t-testi

Testillä selvitetään, onko kahden toisistaan riippumattoman ryhmän tai otoksen välillä merkitsevää eroa.

Esimerkkejä tutkimuskysymyksistä

• • Eroavatko naisten ja miesten palkat keskimäärin toisistaan?
  • Kasvoivatko kahdella eri lannoitteella käsitellyt kasvit keskimäärin erikokoisiksi?
  • Lyhentääkö sinkkitablettien nauttiminen flunssan kestoa?

Oletukset

• • Riippuva muuttuja (palkka, kasvien koko, flunssan kesto) on mitattu välimatka- tai suhdeasteikolla -> Jos näin ei ole, katso Mann-Whitneyn U- testi.
  • Muuttuja on (likimain) normaalijakautunut TAI otoskoko on suuri (jakauman vinoudesta riippuen 30-40 ryhmää kohti). Normaalijakaumaoletusta kannattaa arvioida piirtämällä aineistosta histogrammi ja vertaamalla sen muotoa Gaussin käyrään. -> Jos muuttuja ei ole normaalijakautunut tai otoskoko on pieni, katso Mann-Whitneyn U-testi.
  • Ryhmiä on kaksi -> Jos enemmän, katso ANOVA.
  • Otokset ovat toisistaan riippumattomia – > Jos eivät, katso kahden riippuvan otoksen t-testi.

Esimerkki (PDF) testin suorittamisesta ja testin oikean muodon valitsemisesta

b) Kahden riippuvan otoksen t-testi (t-testi parivertailuille)

Testillä selvitetään, onko kahden riippuvan otoksen välillä merkitsevää eroa. Otokset ovat riippuvia esimerkiksi silloin, jos mitataan samoja henkilöitä kaksi kertaa, vaikkapa ennen käsittelyä ja sen jälkeen.

Esimerkki tutkimuskysymyksestä

• • Ovatko koehenkilöt pidempiä aamulla kuin illalla?

Oletukset

• • Samat kuin kahden riippumattoman otoksen t-testille otosten riippumattomuutta lukuun ottamatta.

Esimerkki (PDF) testin suorittamisesta

c) Mann-Whitneyn U-testi

Mann-Whitneyn testillä selvitetään, onko kahden toisistaan riippumattoman ryhmän tai otoksen välillä merkitsevää eroa.

Esimerkkejä tutkimuskysymyksistä

• • Mann-Whitneyn U-testillä voi tutkia samoja tutkimuskysymyksiä kuin kahden riippumattoman otoksen t- testilläkin.
  • Lisäksi voidaan tutkia järjestysasteikollisia muuttujia, eli esimerkiksi sitä, eroavatko alakoululaisten ja yläkoululaisten kouluruoalle antamat arvosanat toisistaan.

Oletukset

• • Riippuva muuttuja on mitattu järjestys-, välimatka- tai suhdeasteikolla.
  • Ryhmät tai otokset ovat toisistaan riippumattomia.

Mann-Whitneyn U-testin laskeminen Excelillä on melko työlästä. Testi löytyy kaikista tilasto-ohjelmista, tai jos sellaista ei ole käytössä, voi käyttää apuna jotakin netistä löytyvää laskuria, esimerkiksi Saarlandin yliopiston sivuston laskuria (linkki verkkosivulle).

d) ANOVA eli varianssianalyysi

Varianssianalyysiä käytetään, kun halutaan vertailla useampaa kuin kahta riippumatonta ryhmää. Kahden otoksen välinen vertailu suoritetaan t-testillä, mutta jos otoksia on useita, vertailua ei kannata tehdä käyttämällä t-testiä aina kahteen ryhmään kerrallaan. Tällöin tulee helposti hylänneeksi tapauksen, joka olisikin merkitsevä. (Salonen 2018.)

Oletukset

• • Riippuva muuttuja on mitattu välimatka- tai suhdeasteikolla.
  • Muuttuja on (likimain) normaalijakautunut tai otoskoko on suuri (jakauman vinoudesta riippuen 30-40 ryhmää kohti).
  • Otokset ovat toisistaan riippumattomia.
  • Ryhmien varianssit ovat samaa suuruusluokkaa.

Esimerkki (PDF) testin suorittamisesta ja tulosten tulkinnasta

4. Tilastollinen riippuvuus ja korrelaatio

Korrelaatio tarkoittaa kahden muuttujan välistä lineaarista (suoraviivaista) tilastollista riippuvuutta. Matemaattisesti riippuvuutta voidaan mitata laskemalla jokin korrelaatiokerroin. Jos muuttujien välillä on voimakas korrelaatio, niin toisen muuttujan arvot voidaan melko tarkasti päätellä, jos ensimmäisen muuttujan arvot tunnetaan (Salonen 2018). Korrelaatio voi olla joko positiivista tai negatiivista. Positiivinen korrelaatio tarkoittaa, että muuttujan 1 arvojen kasvaessa (pienentyessä) myös muuttujan 2 arvot kasvavat (pienentyvät). Jos muuttujien välillä on negatiivinen korrelaatio, niin muuttujan 2 arvot pienentyvät muuttujan 1 arvojen kasvaessa (tai päinvastoin).

Riippuvuutta on myös muunlaista kuin lineaarista. Esimerkiksi kappaleen liike-energia on suoraan verrannollinen nopeuden toiseen potenssiin, mutta liike-energian ja nopeuden välillä ei ole lainkaan korrelaatiota. Korrelaatio mittaa ainoastaan lineaarista riippuvuutta, eikä sen puuttuminen siis välttämättä tarkoita, että muuttujat olisivat toisistaan riippumattomia. Lisäksi tulee pitää mielessä, että korrelaatio ei ole sama asia kuin syy-seuraussuhde. Klassinen esimerkki tästä on jäätelönsyönnin ja hukkumisten vahva korrelaatio: Molemmat ovat kesällä yleisempiä kuin talvella. Tämä ei kuitenkaan johdu siitä, että jäätelönsyönti aiheuttaisi hukkumisia, vaan siitä, että molemmat ovat yleisempiä lämpimällä kuin kylmällä säällä.

Graafisesti korrelaatiota voidaan tutkia piirtämällä pistediagrammi kahden muuttujan havaittujen arvojen pareista. Kuvio kannattaa aina piirtää, vaikka laskisikin korrelaatiokertoimen. Pistediagrammi antaa oleellista tietoa korrelaatiokertoimen tulkinnan kannalta tai voi toisaalta antaa viitteitä siitä, että muuttujien välillä on epälineaarinen riippuvuussuhde.

Pearsonin korrelaatiokerroin

Yleisimmin käytetty mittari korrelaatiolle on Pearsonin korrelaatiokerroin. Se kuvaa kahden vähintään välimatka-asteikolla mitatun muuttujan suoraviivaista riippuvuutta. Pearsonin korrelaatiokerroin voi saada arvoja lukujen -1 ja +1 välillä. Lukuarvo 0 tarkoittaa, ettei muuttujien välillä ole lineaarista riippuvuutta. Ääriarvoja vastaavat korrelaatiokertoimet tarkoittavat täydellistä negatiivista (-1) tai positiivista (+1) lineaarista riippuvuutta.

Korrelaatiokerroin poikkeaa usein nollasta, mikä voi kuitenkin johtua myös sattumasta. (Salonen 2018.) Tästä syystä korrelaatiokerrointa laskettaessa tehdäänkin yleensä samalla myös tilastollinen testaus, jossa tutkitaan, poikkeaako korrelaatiokerroin merkitsevästi nollasta. Merkitsevyyden testaaminen edellyttää, että muuttujat ovat likimain normaalijakautuneita, tai että otoskoko on riittävän suuri (vähintään noin 25-30). Katso esimerkki (PDF) Pearsonin korrelaatiokertoimen määrittämisestä ja raportoimisesta.

Aineiston ja tulosten visualisointi

Tutkimustulosten ja aineiston esittelyssä kannattaa tarvittaessa käyttää taulukoita ja kuvioita, mutta näitäkin on hyvä käyttää maltillisesti. Usein taulukoissa tuodaan esille numeerisia tuloksia, ja niiden avulla tulokset voi esittää lyhyemmässä muodossa. Silloin varsinaisessa tekstissä ei enää ole mielekästä toistaa samoja asioita, vaan keskittyä tärkeimpien esiin nostamiseen ja tulkintaan. Taulukoiden ja kuvioiden tavoitteena on selkeyttää tuloksia, joten niiden suunnitteluun ja luettavuuteen kannattaa panostaa. On kuitenkin pidettävä mielessä, että tulosten raakadatan paikka ei ole varsinaisessa tekstissä, vaan sen voi halutessaan lisätä raportin liitteisiin.  

Kuvioilla voi hyvin havainnollistaa tutkimustuloksia, sillä niihin pystyy helposti tiivistämään paljon tietoa ja ne antavat nopeasti yleiskäsityksen ilmiöstä (Nummenmaa 2009). Kuvioita ovat kaikki muut raportin havainnollistamiskeinot paitsi taulukot (Hirsjärvi et al. 2013). Kuvioita kannattaa myös pohtia tarkkaan: Ovatko kaikki tarpeellisia? Mitä lisäarvoa ne tuovat raportille? Tutkimustuloksia voi havainnollistaa selkeillä pylväs- tai sektoridiagrammeilla. Diagrammin valinnassa ja laadinnassa tulee olla huolellinen. Kuvaajissa ei suositella käytettäväksi kovinkaan paljon värejä, vaan taustan tulisi olla valkoinen ja itse kuvaaja hyvin erottuvalla perusvärillä, esim. musta tai sininen (Nummenmaa 2009). 

Kaikki taulukot ja kuviot tulee numeroida ja nimetä. Jos taulukko tai kuvio on lainattu muusta lähteestä, lähde on aina merkittävä. 

 Tehtävä: tulosten visualisointi 

Miten tutkimustulokset on esitetty tutkimuksessa Vanhemmat alkoholin välittäjinä? Miten tulosten esittämisessä on onnistuttu?

Katso lisää vinkkejä ja käytännön ohjeita tulosten visualisoimiseen sekä kuvaajien tekemiseen Tiedelukutaidon perusteet -kurssin luvusta Tutkimusaineiston visualisointi.

Lähteet:

Hirsjärvi, S., Remes, S. & Sajavaara, P. 2013. Tutki ja kirjoita. Helsinki: Tammi.

Mellin, I. 2007. Tilastolliset menetelmät. Teknillinen korkeakoulu.

Nummenmaa, L. 2009. Käyttäytymistieteiden tilastolliset menetelmät. Helsinki: Tammi. 

Saaranen-Kauppinen, A. & Puusniekka, A. 2006. KvaliMOTV – Menetelmäopetuksen tietovaranto [verkkojulkaisu]. Tampere: Yhteiskuntatieteellinen tietoarkisto [ylläpitäjä ja tuottaja]. <http:// www.fsd.uta.fi/menetelmaopetus/>. Luettu 07.08.2017.

Salonen, V. 2018. Opinkirjolle koottu materiaalipaketti.